交流電阻和阻抗
以歐姆為單位的阻抗是對包含電阻和電抗的交流電路的電流的有效阻抗。
我們在之前的教程中已經看到,在包含正弦波形的交流電路中,電壓和電流相量以及複數可用於表示複數量。
我們還看到先前在時域變換中繪製的正弦波形和函式可以被轉換為空間或相量域,從而可以構造相量圖以找到電壓 - 電流相量關係。
現在我們知道如何將電壓或電流表示為相量,我們可以在連線到單相交流電源時應用於基本無源電路元件(如交流電阻) 時檢視這種關係。
任何理想的基本電路元件,如電阻器,都可以在電壓和電流方面進行數學描述,在關於電阻器的教程中,我們看到純歐姆電阻器兩端的電壓與流過它的電流成線性比例,如下所示:歐姆定律。考慮下面的電路。
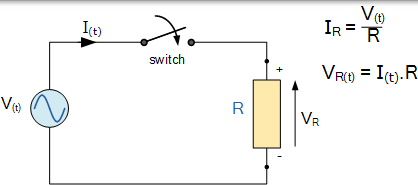
具有正弦電源的交流電阻

當開關關閉時,交流電壓 V 將被施加到電阻器 R。該電壓將導致電流流動,隨著施加的電壓上升和下降,電流將上升和下降。由於負載是電阻,電流和電壓都將達到它們的最大值或峰值,並在完全相同的時間下降到零,即它們同時上升和下降,因此被稱為同相。
然後,流過交流電阻的電流隨時間正弦變化,並由表示式 I(t)= Im x sin(ωt+θ) 表示,其中 Im 是電流的最大幅度,θ 是其相位角。此外,我們還可以說,對於任何給定的電流 I 流過電阻器,R 端子上的最大或峰值電壓將由歐姆定律給出:
$$ \mathrm { V } _ { ( \mathrm { t } ) } = \mathrm { R.I } _ { ( \mathrm { t } ) } = \mathrm { R } \cdot \mathrm { I } _ { \mathrm { m } } \sin ( \omega \mathrm { t } + \theta ) $$
電流的瞬時值將是:
$$ i _ { R ( t ) } = I _ { R ( \max ) } \sin \omega t $$
因此,對於純電阻電路,流過電阻器的交流電流與沿其施加的電壓成比例地變化,遵循相同的正弦模式。由於供電頻率對電壓和電流都是共同的,它們的相量也是共同的,導致電流與電壓同相(θ= 0)。
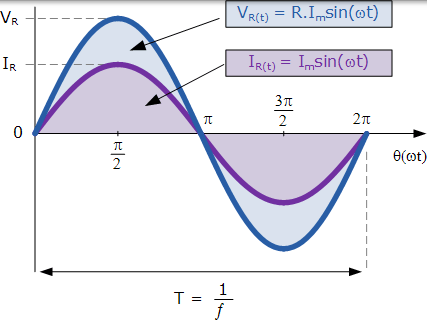
換句話說,當使用交流電阻時,電流和電壓之間沒有相位差,因為只要電壓達到其最大值,最小值和零值,電流將達到其最大值,最小值和零值,如下所示。
交流電阻的正弦波形
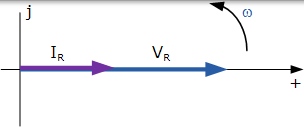
這種“同相”效應也可以用相量圖表示。在複數域中,阻力是實數,僅意味著沒有 j 或虛數分量。因此,當電壓和電流彼此同相時,它們之間將不存在相位差( θ= 0),因此每個量的向量沿著相同的參考軸被相互疊加。從正弦時域到相量域的轉換為,
交流電阻的相量圖
相量代表電流或者電壓的 RMS 值,它不像向量那樣表示峰值或最大值,它將時域表示式的峰值除以 √2 來得到 有效值或者 RMS 值,對應的電壓-電流相量關係為,
RMS 關係
$$ \begin{array} { c } { \mathrm { I } = \frac { \mathrm { I } _ { \mathrm { m } } } { \sqrt { 2 } } \angle \theta \mathrm { A } \quad \text { and } \quad \mathrm { V } = \frac { \mathrm { R } \cdot \mathrm { I } _ { \mathrm { m } } } { \sqrt { 2 } } \angle \theta \mathrm { V } } \\ { \therefore \mathrm { R } = \frac { \mathrm { V } } { \mathrm { I } } = \frac { \left( \mathrm { R.I } _ { \mathrm { m } } / \sqrt { 2 } \right) \angle \theta } { \left( \mathrm { I } _ { \mathrm { m } } / \sqrt { 2 } \right) \angle \theta } } \end{array} $$
相位關係
$$ \begin{array} { c } { \mathrm { V } = \mathrm { R } . \mathrm { I } _ { \mathrm { RMS } } \angle \theta \quad \text { and } \quad \mathrm { I } = \mathrm { I } _ { \mathrm { RMS } } \angle \theta } \\ { \mathrm { V } \angle \theta _ { \mathrm { v } } = \mathrm { I } \angle \theta _ { \mathrm { i } } } \\ { \therefore \theta _ { \mathrm { v } } = \theta _ { \mathrm { i } } ( \mathrm { in } - \text { phase } ) } \end{array} $$
這表明 AC 電路內的純電阻產生其電壓和電流相量之間的關係,其方式與 DC 電路中相同的電阻器電壓和電流關係完全相同。然而,在直流電路中,這種關係通常被稱為電阻,如歐姆定律所定義那樣,但在正弦交流電路中,這種電壓 - 電流關係現在稱為阻抗。換句話說,在 AC 電路中,電阻被稱為阻抗。
在這兩種情況下,這種電壓 - 電流( VI)關係在純電阻中始終是線性的。因此,當在交流電路中使用電阻器時,通常使用阻抗一詞,符號 Z 來表示其電阻。因此,我們可以這樣來說,對於一個電阻器,直流電阻= AC 阻抗,或 R = Z。
對於 AC 電阻值,阻抗向量由字母( Z) 表示,其中歐姆( Ω)的單位與 DC 相同。然後阻抗(或交流電阻)可以定義為:
AC 阻抗
$$ Z = \frac { V } { I } (\Omega) $$
阻抗也可以用複數表示,因為它取決於電路的頻率 ω,當存在無功分量時。但在純電阻電路的情況下,該無功分量將始終為零,並且作為複數給出的純電阻電路中阻抗的一般表示式為:
Z = R + j0 =R (Ω)
由於純電阻交流電路中電壓和電流之間的相角為零,因此功率因數也必須為零,並給出如下: cos 0o = 1.0,然後電阻器消耗的瞬時功率由下式給出:
$$ \mathrm { P } = \mathrm { V.I } = \mathrm { V } _ { \mathrm { m } } \sin \omega \mathrm { t } \times \mathrm { I } _ { \mathrm { m } } \mathrm { sin \omega t } = \mathrm { V } _ { \mathrm { m } } \mathrm { I } _ { \mathrm { m } } \sin ^ { 2 } \omega \mathrm { t } \\ \therefore P _ { \max } = \sin ^ { 2 } ( \omega \mathrm { t } ) , \quad \text { where } \mathrm { P } _ { \max } = \mathrm { V } _ { \max } \mathrm { I } _ { \max } $$
然而,由於電阻或電抗電路中的平均功率取決於相角,而在純電阻電路中,這等於 θ= 0,功率因數等於 1,因此可以定義 AC 電阻消耗的平均功率只需使用歐姆定律:
$$ \mathrm { P } = \mathrm { V.I } = \mathrm { I } ^ { 2 } \mathrm { R } = \frac { \mathrm { V } ^ { 2 } } { \mathrm { R } } \text { watts } $$
同直流電路相同的歐姆定律方程。然後,AC 電阻消耗的有效功率等於 DC 電路中相同電阻器消耗的功率。
許多 AC 電路(例如加熱元件和燈)僅由純歐姆電阻組成,並且具有可忽略的電感值或電容值。
在這樣的電路中,我們可以使用歐姆定律,基爾霍夫定律以及簡單的電路規則來計算和查詢直流電路分析中的電壓,電流,阻抗和功率。使用此類規則時,通常僅使用 RMS 值。
交流電阻示例 No1
交流電阻為 60 歐姆的電加熱元件連線在 240V AC 單相電源上。計算從電源電流和加熱元件消耗的功率。繪製相應的相量圖,顯示電流和電壓之間的相位關係。
- 供電電流:
$$ I = \frac { V } { R } = \frac { 240 } { 60 } = 4.0 A $$
- 交流電阻消耗的有功功率計算如下:
$$ \mathrm { P } = \mathrm { I } ^ { 2 } \mathrm { R } = 4 ^ { 2 } .60 = 960 \mathrm { W } $$
- 由於電阻分量中沒有相位差( θ= 0),相應的相量圖如下:

交流電阻示例 No2
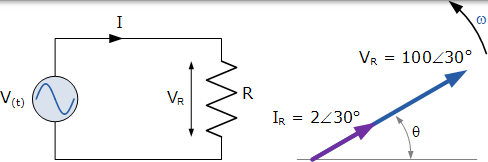
V(t)= 100 x cos(ωt+ 30o) 的正弦電壓電源連線到 50 歐姆的純電阻上。確定其阻抗和流過電路的電流峰值。繪製相應的相量圖。
電阻兩端的正弦電壓與純電阻電路中的電源相同。將此電壓從時域表示式轉換為相量域表示式,可以得到:
$$ \mathrm { V } _ { \mathrm { R } ( \mathrm { t } ) } = 100 \cos \left( \omega \mathrm { t } + 30 ^ { \circ } \right) \quad \Rightarrow \quad \mathrm { V } _ { \mathrm { R } } = 100 \angle 30 ^ { \circ } \mathrm { volts } $$
應用歐姆定律後,
$$ \mathrm { I } _ { \mathrm { R } } = \frac { \mathrm { V } _ { \mathrm { R } } } { \mathrm { R } } = \frac { 100 \angle 30 ^ { \circ } } { 50 \Omega } = 2 \angle 30 ^ { \circ } \mathrm { Amps } $$
因此相應的相量圖將是:
阻抗總結
在純歐姆交流電阻中,電流和電壓都是同相的,因為它們之間沒有相位差。流過電阻的電流與其兩端的電壓成正比,在 AC 電路中這種線性關係稱為阻抗。
在純歐姆電阻中阻抗 Z 是僅由實數部分(實際 AC 電阻值 R )和零虛部( j0)組成的複數。因此,歐姆定律可用於包含交流電阻的電路中,以計算這些電壓和電流。
在下一個關於交流電感的教程中,我們將研究當穩態正弦交流波形施加於其上時電感器的電壓 - 電流關係以及純電感和非純電感的相量圖表示。